MATH 315 Fall 2024 MATLAB Exploratory 1

                                              

Computer Modeling of Plant Growth

 

 

If you have not already done so, download and install MATLAB on your own computer. Click here for details on how to do this. Review the basic features of MATLAB.  The Getting Started with MATLAB video should be useful.

 

The name MATLAB  stands for Matrix Laboratory. The American mathematician Cleve Moler (born August 17, 1939) created MATLAB  in the late 1970’s to assist his students at Stanford and the University of New Mexico. Moler cofounded the company MathWorks to commercialize this software. The MathWorks website features hundreds of useful links.

 

            In  this exploratory, we will focus on the foxglove (Digitalis purpurea) example 10.3 of Causton. Recall that the number, y, of plants surviving at time t (measured in months from the emergence of the seedlings) was given by the equation

            Show first (paper and pencil exercise) that

and hence that y  satisfies the differential equation

  with yo = y(0) =100.

Rewriting the differential equation as

 

we observe that the foxglove population decreases at a constant percentage rate.

            Conversely, you saw in first year calculus, that if y is any quantity that grows (positively or negatively) at a constant percentage rate, so that  y satisfies the equation y'/y = k, then y must have the form  (You may wish to review, at your leisure, the derivation of this fact).

 

            We are going (temporarily!) to forget this little bit of mathematics and use MATLAB to investigate the behavior of the foxglove population, assuming only that its initial population is 100 and that it decreases at a constant  percentage rate, 23.1%. MATLAB has the capacity to solve analytically many commonly occurring differential equations producing a closed form answer. Most differential equations arising as models of real world situations, particularly nonlinear systems, do not possess closed form answers we can find.  Thus, algorithms to provide approximate numerical solutions are critically important. MATLAB  has many different numerical methods built in, some of which we will explore in this course. For now, we will focus on perhaps the simplest scheme: Euler’s Method.

 

The Euler method This method, introduced by the great Swiss mathematician Leonhard Euler (1707 -1783), is based on a simple geometric interpretation of the derivative.

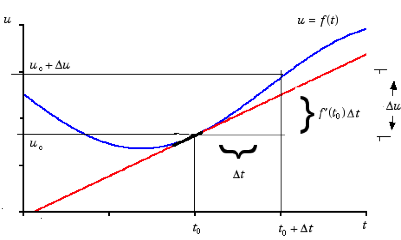
Suppose that u = f(t) is a differentiable function of t and that the value of the function and its first derivative are known at a number  t0 . We wish to approximate the value of the function at a nearby number to + ∆t. Direct computation may be quite difficult. Note, however, that the graph of the tangent line to the curve u = f(t) stays close to the curve near a point of tangency (to,f(to)) = (to, uo). The slope of the tangent line is given as f'(to) = u'(to, uo). It is a simple matter to use the equation of the tangent line to find the point on that line with first coordinate equal to to + ∆t. If ∆t is small, then the second coordinate of this point is a good approximation to the value f(to + ∆t ) since the tangent line will not wander far from the curve (see Figure 1 below). The smaller ∆t is, of course, the better the approximation will be. Analytically, the actual change in the function from  to to to + ∆t is

 

∆u  = f(to + ) - f(to) = f(to + ) -f(to)

 

The approximation is that ∆u  is roughly equal to f '(to )  so that

f(to + ) ~ uo  + f '(to)   

 

which may also be written as

f(to + ∆t) ~ uo  + u'(to , uo ) ∆t, 

 

where ~ is a symbol representing "approximately equal to."

s\

Figure 1. We approximate the change in height of the graph of a function near the point of tangency by the change in height of the tangent line. '

___________________________________________________                             

EXAMPLE    Suppose u = f(t) = and to = 4. Then uo = = 2 and f'(t) =  so that f'(to) = f'(4) = u'(4,2) = = . The approximation that is made here is

~ 2 + ∆t

 

If we wish to compute  for example, then we take ∆t = .41. The approximate value is 2 + = 2.1025. The actual value of  is 2.100. The approximation here is quite good.

___________________________________________________                             

 

Many calculus texts contain detailed discussion of this method of "increments" for approximations. See, for example, Section 2.8, “Linear Approximations and Differentials” in Swokowski, Olinick and Pence’s Calculus,  Sixth Edition (Boston: PWS,  1994).

The method of increments is the basis for Euler's technique of approximating solutions to differential equations.

 

 In the context of the foxglove model,    which has the form  suppose the initial level of foxgloves is  y0. Then the rate of change is    . In a short time interval ∆t, the amount ∆y that the foxglove population will change is approximately   

 

Thus at time t1 = to + ∆t = 0 + ∆t = ∆t, the new foxglove  population level will be approximately

If we choose ∆t  to be small, then the estimated coordinates will be quite close to the actual coordinates at time ∆t.

            Once a new population has been estimated, it may be treated as the initial point of the system and the method of increments can be applied again. This may be done as often as you like. The general formula for estimating successive populations  would be

 

 

t

 

 

1.      Your first task is to create a MATLAB program to implement Causton’s example. Choose a step size   of 1 to begin and plot the numerical approximation over the time interval from 0 to 15 months. Compare the plot of the numerical approximations to the  plot of the actual solution.
It should be fun to create a LiveScript from scratch, but if you get stuck, you might modify the MATLAB file Euler_Method_Example.mix which you can download from the Handouts folder on our course website.

2.   Run your program with some smaller and larger sizes for     (suggestions: .025, .001, 2.0) and compare the results.

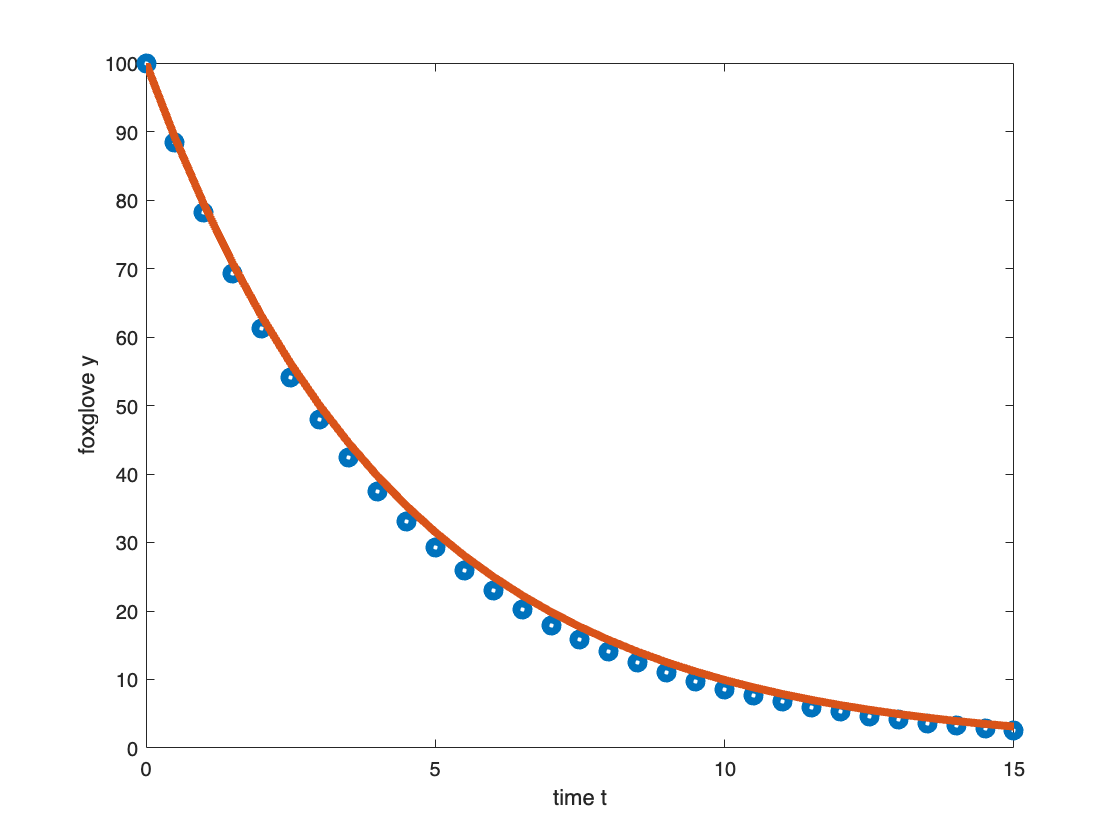
3.   For   = 0.5, display a plot which shows the graphs of the Euler Method estimated values and the exact values for the foxglove population. Your plot will probably look something like

A graph of a function Description automatically generated

For   = 0.5, display a table which shows the Euler Method estimated values and the exact values for the foxglove population at each month. Your table will probably look something like

 

Month

Estimated_Foxglove

Exact_Foxglove

 

0

100

100

 

1

78.234

79.374

 

2

61.206

63.002

 

3

47.884

50.007

 

4

37.461

39.693

 

5

29.307

31.506

 

6

22.928

25.007

 

7

17.938

19.849

 

8

14.033

15.755

 

9

10.979

12.506

 

10

8.5893

9.9261

 

11

6.7197

7.8788

 

12

5.2571

6.2537

 

13

4.1129

4.9638

 

14

3.2177

3.94

 

15

2.5173

3.1273

 

 

4.         Renewing the population.    New foxgloves may be added to the population by external forces (a gardener, for example)  Investigate the number of living foxglove plants if the gardener adds 10 new plants each month.  The differential equation representing this situation would be   Without solving the differential equation, show that  Modify your MATLAB file to use Euler’s Method to plot the estimated foxglove over a long period of time. Do some simulations with initial y value well above 43.29 and others with a much smaller positive value below 43.29.


5.         Explain why  and  are not solutions of the differential equation  . Use techniques from elementary calculus to find a correct closed form solution. You can also find a solution method in Chapter 2 of the Brannan & Boyce differential equations text.

 

 

 

         If you are anxious to learn more about other numerical methods for solving differential equations, take a look at Chapter 8 of Brannan and Boyce.